很多朋友对于欧式看涨期权价格公式和欧式看涨期权定价公式的推导不太懂,今天就由小编来为大家分享,希望可以帮助到大家,下面一起来看看吧!
本文目录一览:
- 〖壹〗、写出欧式看涨期权和看跌期权平价公式并给出证明
- 〖贰〗、如何理解black-scholes期权定价模型?
- 〖叁〗、期权定价公式是怎样的?
- 〖肆〗、费用中N值、X值是什么意思?
- 〖伍〗、看涨期权看跌期权平价定理是什么?
- 〖陆〗、求~期权公式代码含义
- 〖柒〗、期权的价值计算公式,期权的权利金计算公式
写出欧式看涨期权和看跌期权平价公式并给出证明
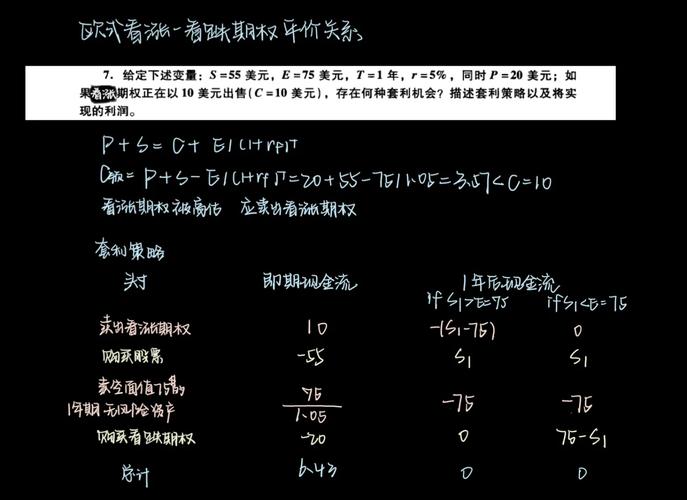
〖壹〗、C+Ke^(-rT)=P+S0 平价公式是根据无套利原则推导出来的。构造两个投资组合。看涨期权C,行权价K,距离到期时间T。现金账户Ke^(-rT),利率r,期权到期时恰好变成K。看跌期权P,行权价K,距离到期时间T。标的物股票,现价S0。看到期时这两个投资组合的情况。
〖贰〗、B: 一个看跌期权和一股标的股票,看跌期权的行权费用=X,股票费用为S 投资组合A的费用为:看涨期权费用(C)+无风险债券费用(PV(X)。PV(X)为债券现值。投资组合B的费用为:看跌期权费用(P)+股票费用S 画图或者假设不同的到期情况可以发现,A、B的收益曲线完全相同。
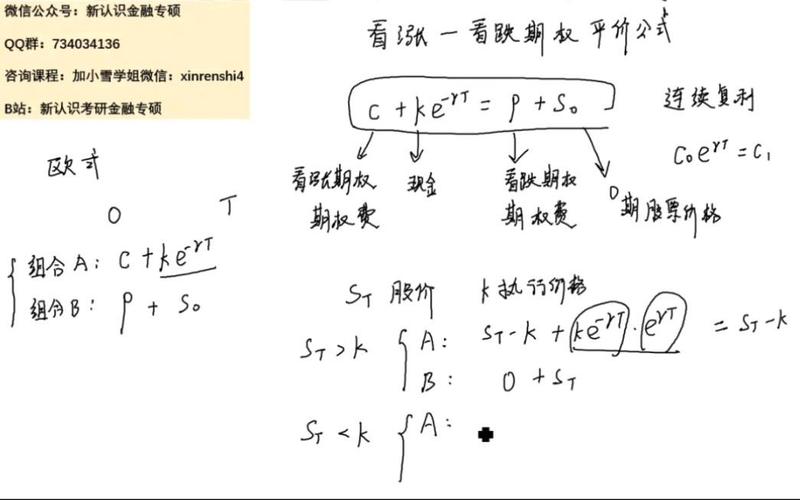
〖叁〗、期权平价公式:C+ Ke^-r(T-t)=P+S。公式含义:认购期权费用C与行权价K的现值之和等于认沽期权的费用P加上标的证券现价S。符号解释:T-t:还有多少天合约到期;e的-r(T-t)次方是连续复利的折现系数;Ke^-r(T-t):K乘以e的-r(T-t)次方,也就是K的现值。
〖肆〗、美式期权的看涨看跌期权平价关系 美式期权看涨费用等于欧式费用,看跌费用大于等于欧式,构建组合E和F,得出无收益资产的美式期权平价公式。美式期权平价关系进一步推导 详细推导过程略,结果得出无收益资产美式期权平价公式。
如何理解black-scholes期权定价模型?
Black-Scholes 期权定价模型是一种用于计算欧式期权费用的数学模型,它是由费希尔·布莱克(Fisher Black)和米伦·斯科尔斯(Myron Scholes)在1973年开发的。这个模型是建立在对股票费用的对数正态分布假设、无风险利率、标的资产的波动率和期权到期时间等基本假设的基础之上的。
他们创立和发展的布莱克—斯克尔斯期权定价模型(Black-Scholes Option Pricing Model)为包括股票、债券、货币、商品在内的新兴衍生金融市场的各种以市价费用变动定价的衍生金融工具的合理定价奠定了基础。
理解Black-Scholes期权定价模型,需要从金融产品的本质出发,即预期、承诺和兑现未来的现金流。我们可以将一个金融产品,如欧式看涨期权,视为在未来特定时间可以实现的现金流的预期现值。在解释模型之前,我们先回顾一下基本的概念,如连续复利和如何进行贴现。

期权定价公式是怎样的?
期权定价公式,尤其是Black-Scholes期权定价模型,是计算期权费用的数学公式。该模型由Fischer Black和Myron Scholes于1973年提出。对于欧式看涨期权,公式为:C = S0 * N(d1) X * e^(-rt) * N(d2);对于欧式看跌期权,公式为:P = X * e^(-rt) * N(-d2) S0 * N(-d1)。
期权定价公式是Black-Scholes公式,它表示期权费用是由股票费用、期权的执行费用、期权的有效期、无风险利率以及股票的波动率所决定的。这个公式是由Fisher Black和Myron Scholes在1973年提出的,并成为了期权定价的基础。
期权定价公式是:期权费用=内在价值+时间价值。期权定价模型,由布莱克与斯科尔斯在20世纪70年代提出。该模型认为,只有股价的当前值与未来的预测有关;变量过去的历史与演变方式与未来的预测不相关 。
费用中N值、X值是什么意思?
X为期权到期日当天的股票行权价;t为以年为单位表示的期权合约剩余期限;r为市场上的无风险利率水平;N(.)为累积标准正态分布函数,即经风险调整后的概率值。该公式将欧式看涨期权的损益分为两个部分:期权到期日当天股票被行权后收到的金额;期权合约期间内持仓股票的价值。
M代表MinimumCharge,即最低运费。N代表NormalRate,指45公斤以下普通货物的运价。Q则表示QuantityRate,适用于45公斤以上的分量普通货物的运价。B指的是BasicCharge,仅适用于欧盟国家之间的运输。K表示RateperKilogramme,即每公斤运价,同样仅适用于欧盟国家之间。
正态分布,简称N,是概率论中的核心概念。它由两个关键参数定义:一是数学期望,也就是我们通常说的均值,它代表了随机变量取值的中心位置;二是方差,它是衡量数据分散程度的指标,方差越大,数据的波动性越强,反之则越稳定。在正态分布中,这两个参数决定了分布的形状和位置。
补偿或赔偿计算。n=nx这个公式通常用于商业中的补偿或赔偿计算。其中,n代表需要补偿或赔偿的数量,x代表每个数量的补偿或赔偿标准。因此,n=nx的意思是,需要补偿或赔偿的数量n乘以每个数量的补偿或赔偿标准x,得到最终的补偿或赔偿金额。
偏度的计算主要基于数据的3阶矩定义,其计算公式为:Sk = (n / (n - 1) * (n - 2)) * Σ(xi - x)^3 / σ^3),其中n表示观测值的数量,xi表示i个观测值,x表示所有观测值的平均数,σ表示所有观测值的标准差。
$mu$ 是总体均值,$x_1, x_2, ldots, x_n$ 是总体中的数值,$n$ 是总体数量。注意:样本标准差在计算时使用了自由度 $n1$,这是因为样本数据是从总体中随机抽取的,需要考虑到样本估计总体时的误差,因此自由度会比样本数量少1。而总体标准差则直接使用总体数量 $n$ 作为分母。

看涨期权看跌期权平价定理是什么?
期权平价公式:C+ Ke^-r(T-t)=P+S。公式含义:认购期权费用C与行权价K的现值之和等于认沽期权的费用P加上标的证券现价S。符号解释:T-t:还有多少天合约到期;e的-r(T-t)次方是连续复利的折现系数;Ke^-r(T-t):K乘以e的-r(T-t)次方,也就是K的现值。
期权平价定理是金融期权理论中的一个基本概念,它表述了期权费用与标的资产费用、到期日和利率之间的关系。简单来说,这个公式C+ Ke^-r(T-t)=P+S表示,一个欧式看涨期权的费用C加上其行权价K按照连续复利折现的现值Ke^-r(T-t),等于同条件下一个欧式看跌期权的费用P,再加上标的证券的现价S。
看涨期权和看跌期权平价定理是:在套利驱动的均衡状态下,购买一股看涨期权、卖空1股股票、抛出1股看跌期权、借入资金购买1股股票的投资组合的收益应该为0 。
看涨期权费用-看跌期权费用=标的资产的费用-执行费用的现值,这种关系,被称为看涨期权-看跌期权平价定理,利用该等式中的4个数据中的3个,就可以求出另外1个。看涨期权是期权赋予持有人在到期日或到期日之前,以固定费用购买标的资产的权利。其授予权利的特征是购买。
平价定理的原理是:在套利驱动的均衡状态下,购买一股看涨期权、卖空1股股票、抛出1股看跌期权、借入资金购买1股股票的投资组合的收益应该为0 。利率平价定理是指在无风险资产和有风险资产之间,市场参与者应该期望收回相等的内部收益率。
看跌期权费用计算方式:看跌期权费用=看涨期权费用+执行费用的现值-股票的费用。

求~期权公式代码含义
以au2104C464期权合约为例,其中au代表的是黄金,2104代表期权到期时间为2021年4月,c代表看涨期权的意思,464则是期权的执行费用。
期权平价公式为:C + Ke^= P + S。其中各符号含义如下:C:表示认购期权的费用。认购期权,又称看涨期权,赋予持有人在某一特定日期或该日之前的任何时间以固定费用购进一种资产的权利。K:表示行权价。行权价是期权合约中规定的,持有人行使权利时购进或售出资产的费用。
期权定价公式是BlackScholes公式。它表示期权费用是由以下因素决定的:股票费用、期权的执行费用、期权的有效期、无风险利率以及股票的波动率。
期权的价值计算公式,期权的权利金计算公式
期权的权利金计算公式:权利金 = 期权价值 × 手数 × 手续费率。这里,期权价值是根据上述期权价值公式计算得出的,手数表示交易的数量,手续费率则是根据交易所规定或期权合约约定确定的。请注意,这些公式和计算方法都是基于一定的假设和条件的,实际应用时可能需要根据具体情况进行调整。
权利金计算公式为:期权价值×手数×手续费率。具体计算方法需参照交易所规定或期权合约约定。
计算公式:买(卖)期权合约需要缴纳的权利金=交易平台上变动的权利金合约张数一张合约所包含的份数。交易平台上展示的权利金是不断变化的,但可以确定的是一张期权里面包含的是一万份(借鉴股票的一手等于100股)。
公式:权利金=期权合约结算价*交易单位 期权权利金的计算公式很简单,就跟股票的买入市值计算方式是一样的,买过一次期权合约就能理解和上手了。
对于期权买方,他们通过支付权利金,换取了在特定时间内执行合约的权利。这个权利金的计算公式相当直观:权利金 = 费用 × 合约乘数,简单明了,只需支付期权合约的固定成本,无需过多计算。卖方的义务与回报 相反,期权卖方则以收取权利金的形式,承担了可能被要求履行合约的义务。
感谢大家聆听我对于欧式看涨期权价格公式的经验分享介绍到此就结束了,希望我的知识可以帮到您。